paxos
一:简介
主要源自《Paxos Made Simple》,对其进行翻译,用自己的思路理解,扩充。
二:内容
除了翻译文章以外,更重要的是自己去理解,然后在联系到实际应用中。或者说,这篇文章给自己带来了什么。
1 问题定义 The Problem
Assume a collection of processes that can propose values. A consensus al-
gorithm ensures that a single one among the proposed values is chosen. If
no value is proposed, then no value should be chosen. If a value has been
chosen, then processes should be able to learn the chosen value. The safety
requirements for consensus are:
• Only a value that has been proposed may be chosen,
• Only a single value is chosen, and
• A process never learns that a value has been chosen unless it actually
has been.
We won’t try to specify precise liveness requirements. However, the goal is
to ensure that some proposed value is eventually chosen and, if a value has
been chosen, then a process can eventually learn the value.
- 只有被提出的value才能被选定。
- 只有一个唯一的value被选定
- 除非一个value已经被chosen,否则其他进程永远不会学习这个值。(意思就是说,只有一个value被确定下来,其他的进程才会去学习该value)
我们的目标是保证最终有一个提出的value被选定。当一个value被选定后,进程最终也能学习到这个value。
用一句简单粗暴的例子,有一群人他们每个人都选择一张扑克牌,最终只有一张让所有的人都认可。这里有一个需要注意的地方,只是选出一个大家都认可的value,使大家都达到一致,并没有任何对错以及业务。
paxos中三种角色,
- Proposer 负责提出proposal
- Acceptor 接收proposal
- Learners 学习已经确定的值
2 选定一个值 Choosing a Value
The easiest way to choose a value is to have a single acceptor agent. A pro-
The easiest way to choose a value is to have a single acceptor agent. A pro-
poser sends a proposal to the acceptor, who chooses the first proposed value
that it receives. Although simple, this solution is unsatisfactory because the
failure of the acceptor makes any further progress impossible.
最简单的方式就是只有一个Acceptor, 这种情况下一定是一致的。但是容灾性很差。
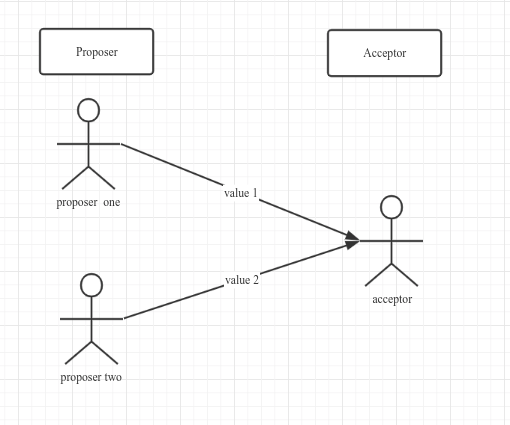
当有多个Acceptor的时候
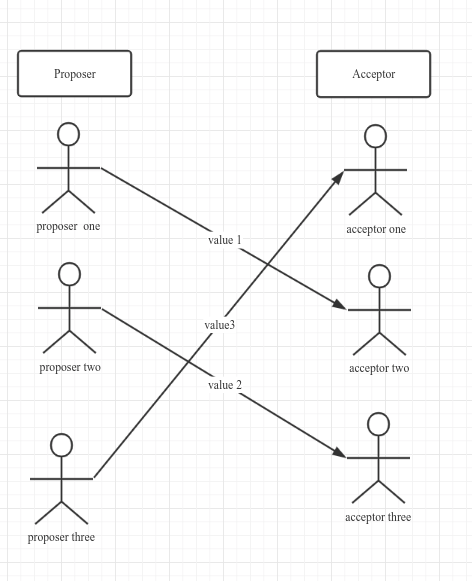
如上图,如果一个proposer只将自己的value发送给一个acceptor,那最终将无法得到一个一致的value.
So, let’s try another way of choosing a value. Instead of a single acceptor,
let’s use multiple acceptor agents. A proposer sends a proposed value to a
set of acceptors. An acceptor may accept the proposed value. The value is
chosen when a large enough set of acceptors have accepted it. How large is
large enough? To ensure that only a single value is chosen, we can let a large
enough set consist of any majority of the agents. Because any two majorities
have at least one acceptor in common, this works if an acceptor can accept
at most one value
每个proposer需要将自己的value发送给一个acceptor集合,这个集合内acceptor的数目必须超过一半。在论文中这个集合叫做多数派,这个多数派必须符合鸽笼原理
we want a value to be chosen
even if only one value is proposed by a single proposer. This suggests the
requirement:
P1. An acceptor must accept the first proposal that it receives.
如果我们希望即使只有一个Proposer提出了一个value,该value也最终被选定。那么,就得到下面的约束:
P1 : 一个Acceptor必须接受收到的第一个proposal(提案)
But this requirement raises a problem. Several values could be proposed by
But this requirement raises a problem. Several values could be proposed by
different proposers at about the same time, leading to a situation in which
every acceptor has accepted a value, but no single value is accepted by a
majority of them. Even with just two proposed values, if each is accepted by
about half the acceptors, failure of a single acceptor could make it impossible
to learn which of the values was chosen.
但是这种约束会产生一个问题,当不同的proposer在同一时间将自己的proposal发送给不同的acceptor的时候,不同的acceptor接收到不同的值,并且没有超过半数的acceptor得到相同value的proposal。 还有一种很极端的情况:所有proposal中只有两个value,但是每个value正好被一半的acceptor接收。
P1 and the requirement that a value is chosen only when it is accepted
P1 and the requirement that a value is chosen only when it is accepted
by a majority of acceptors imply that an acceptor must be allowed to accept
more than one proposal. We keep track of the different proposals that an
acceptor may accept by assigning a (natural) number to each proposal, so a
proposal consists of a proposal number and a value. To prevent confusion,
we require that different proposals have different numbers.
所以,在P1的约束下,如果想要选定一个value,那么必须允许acceptor接收多个proposer的proposal。 此时若要追踪proposal,需要给Proposal特定编号,这里给proposal定义是数据结构是map类型<proposal ID, value>,其中proposal ID是递增序列。
We can allow multiple proposals to be chosen, but we must guarantee
that all chosen proposals have the same value. By induction on the proposal
number, it suffices to guarantee:
我们可以允许选择多个proposal被选定,但是我们必须保证的proposal都具有相同的value。通过对提案编号的归纳,足以保证:
P2. If a proposal with value v is chosen, then every higher-numbered pro-
posal that is chosen has value v .
P2:如果某个value为v的提案被选定了,那么每个编号更高的被选定提案的value必须也是v。
Since numbers are totally ordered, condition P2 guarantees the crucial safety
property that only a single value is chosen.
To be chosen, a proposal must be accepted by at least one acceptor. So,
we can satisfy P2 by satisfying:
由于数字是完全有序的,因此条件P2保证了仅选择一个值的安全性。一个proposal要被选定的话,最少要被一个acceptor接收。 因此,我们可以通过满足以下条件来满足P2:
P2 a . If a proposal with value v is chosen, then every higher-numbered pro-
posal accepted by any acceptor has value v .
P2 a .如果某个value为v的提案proposal被选定了,那么每个编号更高的被Acceptor接受的提案的value必须也是v。 (比如,已知<1,v>被选定了,如果<2,x>要想被acceptor接受,那么此处的x必须要等于v。 这里可以理解为,proposers为了达到一致做出的妥协—将自己原来的提案x替换为v)
We still maintain P1 to ensure that some proposal is chosen. Because com-
munication is asynchronous, a proposal could be chosen with some particu-
lar acceptor c never having received any proposal. Suppose a new proposer
“wakes up” and issues a higher-numbered proposal with a different value.
P1 requires c to accept this proposal, violating P2 a . Maintaining both P1
and P2 a requires strengthening P2 a to:
这里仍然遵循p1(每个acceptor都会接受第一个proposal<serial ID,value>)由于通信是异步的,会产生一些问题。 举一个其他的例子:
假设总共有5个Acceptor。Proposer2提出[M1,V1]的提案,Acceptor2~5(半数以上)均接受了该提案,于是对于Acceptor2~5和Proposer2来讲,它们都认为V1被选定。Acceptor1刚刚从宕机状态恢复过来(之前Acceptor1没有收到过任何提案),此时Proposer1向Acceptor1发送了[M2,V2]的提案(V2≠V1且M2>M1),对于Acceptor1来讲,这是它收到的第一个提案。根据P1(一个Acceptor必须接受它收到的第一个提案。),Acceptor1必须接受该提案。这时Acceptor1认为V2被选定。这样就违背了p2a(因为此时acceptor1选定是v2,而acceptor2~5选定的是v1,且v1 != v2)
所以需要再次加强p2a的约束:
P2 b . If a proposal with value v is chosen, then every higher-numbered pro-
posal issued by any proposer has value v .
P2b:如果某个value为v的提案被选定了,那么之后任何Proposer提出的编号更高的提案的value必须也是v(注意的是,这个角度,是从proposer的角度来约束了,即在众多提案人中,有人需要做出妥协。简单的理解就是只有第一个人提出了自己的提案,其他人都做出了妥协)
Since a proposal must be issued by a proposer before it can be accepted by
an acceptor, P2 b implies P2 a , which in turn implies P 2
因为一个Proposal在被acceptor接收之前必须由一个Proposer提出来。所以p2b可以使p2a成立,进而p2也成立
To discover how to satisfy P2 b , let’s consider how we would prove that
it holds.We would assume that some proposal with number m and value v is chosen and show that any proposal issued with number n > m also has value v . We would make the proof easier by using induction on n, so we can prove that proposal number n has value v under the additional assumption that every proposal issued with a number in m . . (n − 1) has value v , where i . . j denotes the set of numbers from i through j . For the proposal numbered m to be chosen, there must be some set C consisting of a majority of acceptors such that every acceptor in C accepted it. Combiningthis with the induction assumption, the hypothesis that m is chosen implies:
Every acceptor in C has accepted a proposal with number in
m . . (n − 1), and every proposal with number in m . . (n − 1)
accepted by any acceptor has value v .
为了去发现如何满足条件p2b, 让我们先去证明一下怎样使P2b成立。 先假定proposal<m,v>已经被选定了,那么其他的proposal<n,x>(其中n>m)如果要被提出的话,则其提案中的x也必须等于v。通过对n进行归纳,可以使证明更容易,我们可以在附加条件下证明proposal<n,x>中的x=v。 其附加条件为:从提案m~提案n-1,这n-m个提案的内容都为v。(即proposal<m,x> … proposal<n-1,x>,这n-m个proposal的x都等于v)。为了让提案m被选定,必须有一个集合C,(集合C包含了一个多数派的acceptor),它里面的每个成员都接受了这个提案m。将其与归纳假设相结合,选择m的假设意味着:
C中的每一个acceptor都接收了一个编号在m~n-1的proposal,而且每一个编号为m~n-1的proposal的提案内容都是v。
Since any set S consisting of a majority of acceptors contains at least one
member of C , we can conclude that a proposal numbered n has value v by
ensuring that the following invariant is maintained:
上文已经知道了集合C里面已经包含了一个多数派。因此,对于任意一个多数派集合S,它和集合C一定相交。 我们能够得出一个结论:通过遵循以下不变式,能够得到一个编号为n,内容为v的proposal。
P2 c . For any v and n, if a proposal with value v and number n is issued,
then there is a set S consisting of a majority of acceptors such that
either (a) no acceptor in S has accepted any proposal numbered less
than n, or (b) v is the value of the highest-numbered proposal among
all proposals numbered less than n accepted by the acceptors in S .
P2c 对于任何v和n,如果发布了具有v值和n的提案,则存在一个由多数接受者组成的集合S, 一定满足以下两个条件之一 。 (a)S中没有任何acceptor接受任何编号小于n的提案。 条件(b) S中Acceptor接受过的最大编号的提案的value为V。
We can therefore satisfy P2 b by maintaining the invariance of P2 c .
To maintain the invariance of P2 c , a proposer that wants to issue a pro-
posal numbered n must learn the highest-numbered proposal with number
less than n, if any, that has been or will be accepted by each acceptor in
some majority of acceptors. Learning about proposals already accepted is
easy enough; predicting future acceptances is hard. Instead of trying to pre-
dict the future, the proposer controls it by extracting a promise that there
won’t be any such acceptances. In other words, the proposer requests that
the acceptors not accept any more proposals numbered less than n. This
leads to the following algorithm for issuing proposals.
确保约束p2c的话,就能满足p2b。为了维护p2c,一个proposer想要去提交一个编号为n的proposal时,它需要先了解其他已经被选定了的proposal的value,如果之前有proposal被选定的话,就选出这些Proposal中编号小于n的最大值(其实就是向下取最大值。假定其编号为n-1)。如果存在这样的proposal,就将该proposal的value替换成自己即将发布的proposal的value(其实也就是说,只有第一个发出proposal的proposer才能用自己的原本的value,其他的proposer都会妥协,遵循之前的proposer的意志)。
换句话说,proposer要求acceptor不再接受编号小于n的proposal。 这个导致以下用于发布提案的算法。
1. A proposer chooses a new proposal number n and sends a request to each member of some set of acceptors, asking it to respond with:
(a) A promise never again to accept a proposal numbered less than n, and
(b) The proposal with the highest number less than n that it has accepted, if any.
I will call such a request a prepare request with number n.
2. If the proposer receives the requested responses from a majority of
the acceptors, then it can issue a proposal with number n and value
v , where v is the value of the highest-numbered proposal among the
responses, or is any value selected by the proposer if the responders
reported no proposals.
A proposer issues a proposal by sending, to some set of acceptors, a request
that the proposal be accepted. (This need not be the same set of acceptors
that responded to the initial requests.) Let’s call this an accept request.
1) proposer 选择一个编号n,然后发送一个请求给某些acceptor集合中每一个成员,然后等待acceptor的相应。
(a)acceptor承诺不会再去接收编号小于n的proposal
(b) 如果Acceptor已经接受过提案,那么就向Proposer响应已经接受过的编号小于N的最大编号的提案。
我们将该请求称为编号为N的Prepare请求。
2) 如果这个proposer得到了一个多数派acceptor的相应。那么它就能生成一个编号为n,velue为v的提案(即proposal<n,v>)。 这里的V是所有的响应中编号最大的提案的Value。如果所有的响应中都没有提案,那 么此时V就可以由Proposer自己选择。
生成proposal后,Proposer将该proposal发送给某些多数派的Acceptor集合,并期望这些Acceptor能接受该提案。(注意:此时接受Accept请求的Acceptor集合不一定是之前响应Prepare请求的Acceptor集合)
我们称该请求为Accept请求。
This describes a proposer’s algorithm. What about an acceptor? It can
receive two kinds of requests from proposers: prepare requests and accept
requests. An acceptor can ignore any request without compromising safety.
So, we need to say only when it is allowed to respond to a request. It can
always respond to a prepare request. It can respond to an accept request,
accepting the proposal, iff it has not promised not to. In other words:
P1 a . An acceptor can accept a proposal numbered n iff it has not responded
to a prepare request having a number greater than n.
Observe that P1 a subsumes P1.
之前是描述proposer的算法,以下是关于acceptor的算法。acceptor可以从proposer接收两种请求prepare请求和accept请求。一个acceptor可以忽略任何请求而不影响安全性。因此,我们只需要需讨论何时允许响应请求。acceptor始终可以相应prepare请求,如果没有它没有承诺不接受proposal,那么也可以响应accept请求,接受提议。 换句话说, P1a. acceptor可以接受一个编号为n的proposal前提是它之前没有响应过编号大于n的prepare请求。 观察可知,p1a包含了P1
以上已经有了完全的算法,但是还能做一些优化
Suppose an acceptor receives a prepare request numbered n, but it has already responded to a prepare request numbered greater than n, there by promising not to accept any new proposal numbered n. There is then no reason for the acceptor to respond to the new prepare request, since it will not accept the proposal numbered n that the proposer wants to issue. So we have the acceptor ignore such a prepare request. We also have it ignore a prepare request for a proposal it has already accepted.
With this optimization, an acceptor needs to remember only the highest-numbered proposal that it has ever accepted and the number of the highest-numbered prepare request to which it has responded. Because P2 c must be kept invariant regardless of failures, an acceptor must remember this information even if it fails and then restarts. Note that the proposer can always abandon a proposal and forget all about it—as long as it never tries to issue another proposal with the same number
假设acceptor收到编号为n的prepare请求,但已经对编号大于n的prepare请求作出了响应,承诺不接受编号为n的任何新提议。 这样,acceptor就没有理由响应新的prepare请求,因为它不会接受提议者要发布的编号为n的提议。 因此,我们让acceptor忽略这样的prepare请求。 我们也可以忽略它已经接受的提案的prepare请求。
一个Acceptor只需记住:1. 已接受的编号最大的提案 2. 已响应的请求的最大编号。
Phase 1. (a) A proposer selects a proposal number n and sends a prepare
request with number n to a majority of acceptors.
(b) If an acceptor receives a prepare request with number n greater
than that of any prepare request to which it has already responded,
then it responds to the request with a promise not to accept any more
proposals numbered less than n and with the highest-numbered pro-
posal (if any) that it has accepted.
Phase 2. (a) If the proposer receives a response to its prepare requests
(numbered n) from a majority of acceptors, then it sends an accept
request to each of those acceptors for a proposal numbered n with a
value v , where v is the value of the highest-numbered proposal among
the responses, or is any value if the responses reported no proposals.
(b) If an acceptor receives an accept request for a proposal numbered
n, it accepts the proposal unless it has already responded to a prepare
request having a number greater than n.
-
阶段一:
(a) Proposer选择一个提案编号N,然后向半数以上的Acceptor发送编号为N的Prepare请求。
(b) 如果一个Acceptor收到一个编号为N的Prepare请求,且N大于该Acceptor已经响应过的所有Prepare请求的编号,那么它就会将它已经接受过的编号最大的提案(如果有的话)作为响应反馈给Proposer,同时该Acceptor承诺不再接受任何编号小于N的提案。
-
阶段二:
(a) 如果Proposer收到半数以上Acceptor对其发出的编号为N的Prepare请求的响应,那么它就会发送一个针对[N,V]提案的Accept请求给半数以上的Acceptor。注意:V就是收到的响应中编号最大的提案的value,如果响应中不包含任何提案,那么V就由Proposer自己决定。
(b) 如果Acceptor收到一个针对编号为N的提案的Accept请求,只要该Acceptor没有对编号大于N的Prepare请求做出过响应,它就接受该提案。
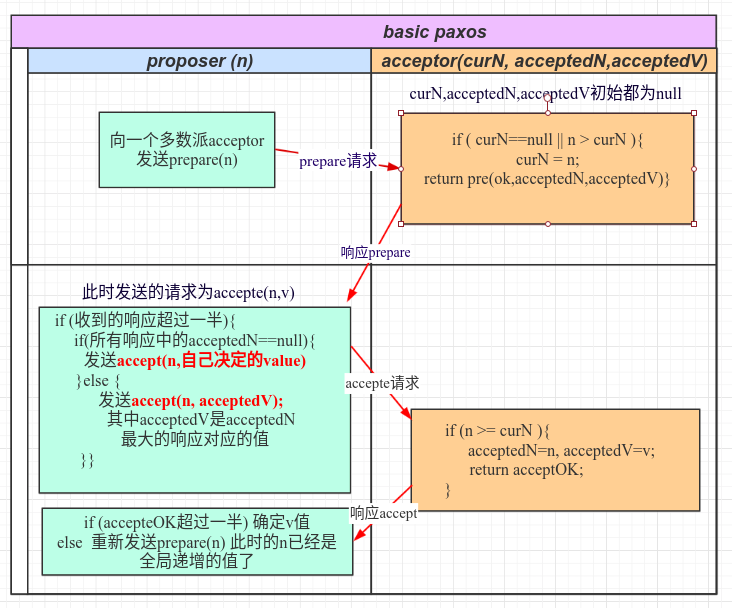
A proposer can make multiple proposals, so long as it follows the algorithm
for each one. It can abandon a proposal in the middle of the protocol at any
time. (Correctness is maintained, even though requests and/or responses
for the proposal may arrive at their destinations long after the proposal
was abandoned.) It is probably a good idea to abandon a proposal if some
proposer has begun trying to issue a higher-numbered one. Therefore, if an
acceptor ignores a prepare or accept request because it has already received
a prepare request with a higher number, then it should probably inform
the proposer, who should then abandon its proposal. This is a performance
optimization that does not affect correctness.
一个提议者可以提出多个提议,只要它遵循每个提议的算法即可,它可以随时在协议中间放弃一个提议。 (即使提案的请求和/或响应可能在提案被放弃后很长时间到达目的地,也保持了正确性。)如果某些提案者已开始尝试发布编号更高的提案,则放弃提案可能是一个好主意。 因此,如果接受者因为已经收到了编号较大的准备请求而忽略了准备或接受请求,则它应该通知提议者,然后由谁放弃提议。 这是不影响正确性的性能优化。
3 例子
假设的3军问题
1) 1支红军在山谷里扎营,在周围的山坡上驻扎着3支蓝军;
2) 红军比任意1支蓝军都要强大;如果1支蓝军单独作战,红军胜;如果2支或以上蓝军同时进攻,蓝军胜;
3) 三支蓝军需要同步他们的进攻时间;但他们惟一的通信媒介是派通信兵步行进入山谷,在那里他们可能被俘虏,从而将信息丢失;或者为了避免被俘虏,可能在山谷停留很长时间;
4) 每支军队有1个参谋负责提议进攻时间;每支军队也有1个将军批准参谋提出的进攻时间;很明显,1个参谋提出的进攻时间需要获得至少2个将军的批准才有意义;
5) 问题:是否存在一个协议,能够使得蓝军同步他们的进攻时间?
接下来以两个假设的场景来演绎BasicPaxos;参谋(proposer)和将军(acceptor)需要遵循一些基本的规则
1) 参谋以两阶段提交(prepare/commit)的方式来发起提议,在prepare阶段需要给出一个编号;
2) 在prepare阶段产生冲突,将军以编号大小来裁决,编号大的参谋胜出;
3) 参谋在prepare阶段如果收到了将军返回的已接受进攻时间,在commit阶段必须使用这个返回的进攻时间;
两个参谋先后提议的场景
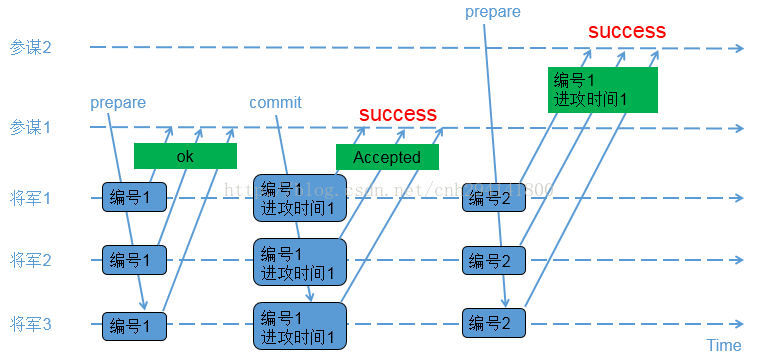
1) 参谋1发起提议,派通信兵带信给3个将军,内容为(编号1);
2) 3个将军收到参谋1的提议,由于之前还没有保存任何编号,因此把(编号1)保存下来,避免遗忘;同时让通信兵带信回去,内容为(ok);
3) 参谋1收到至少2个将军的回复,再次派通信兵带信给3个将军,内容为(编号1,进攻时间1);
4) 3个将军收到参谋1的时间,把(编号1,进攻时间1)保存下来,避免遗忘;同时让通信兵带信回去,内容为(Accepted);
5) 参谋1收到至少2个将军的(Accepted)内容,确认进攻时间已经被大家接收;
6) 参谋2发起提议,派通信兵带信给3个将军,内容为(编号2);
7) 3个将军收到参谋2的提议,由于(编号2)比(编号1)大,因此把(编号2)保存下来,避免遗忘;又由于之前已经接受参谋1的提议,因此让通信兵带信回去,内容为(编号1,进攻时间1);
8) 参谋2收到至少2个将军的回复,由于回复中带来了已接受的参谋1的提议内容,参谋2因此不再提出新的进攻时间,接受参谋1提出的时间;
两个参谋交叉提议的场景
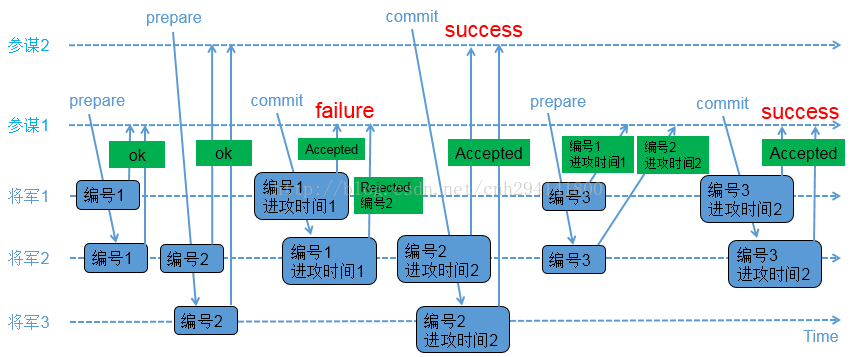
1) 参谋1发起提议,派通信兵带信给3个将军,内容为(编号1);
2) 3个将军的情况如下
a) 将军1和将军2收到参谋1的提议,将军1和将军2把(编号1)记录下来,如果有其他参谋提出更小的编号, 将被拒绝;同时让通信兵带信回去,内容为(ok);
b) 负责通知将军3的通信兵被抓,因此将军3没收到参谋1的提议;
3) 参谋2在同一时间也发起了提议,派通信兵带信给3个将军,内容为(编号2);
4) 3个将军的情况如下
a) 将军2和将军3收到参谋2的提议,将军2和将军3把(编号2)记录下来,如果有其他参谋提出更小的编 号,将被拒绝;同时让通信兵带信回去,内容为(ok);
b) 负责通知将军1的通信兵被抓,因此将军1没收到参谋2的提议;
5) 参谋1收到至少2个将军的回复,再次派通信兵带信给有答复的2个将军,内容为(编号1,进攻时间1);
6) 2个将军的情况如下
a) 将军1收到了(编号1,进攻时间1),和自己保存的编号相同,因此把(编号1,进攻时间1)保存下来; 同时让通信兵带信回去,内容为(Accepted);
b) 将军2收到了(编号1,进攻时间1),由于(编号1)小于已经保存的(编号2),因此让通信兵带信回 去,内容为(Rejected,编号2);
7) 参谋2收到至少2个将军的回复,再次派通信兵带信给有答复的2个将军,内容为(编号2,进攻时间2);
8) 将军2和将军3收到了(编号2,进攻时间2),和自己保存的编号相同,因此把(编号2,进攻时间2)保存下 来,同时让通信兵带信回去,内容为(Accepted);
9) 参谋2收到至少2个将军的(Accepted)内容,确认进攻时间已经被多数派接受;
10) 参谋1只收到了1个将军的(Accepted)内容,同时收到一个(Rejected,编号2);参谋1重新发起提议,派 通信兵带信给3个将军,内容为(编号3);
11) 3个将军的情况如下
a) 将军1收到参谋1的提议,由于(编号3)大于之前保存的(编号1),因此把(编号3)保存下来;由于将 军1已经接受参谋1前一次的提议,因此让通信兵带信回去,内容为(编号1,进攻时间1);
b) 将军2收到参谋1的提议,由于(编号3)大于之前保存的(编号2),因此把(编号3)保存下来;由于将 军2已经接受参谋2的提议,因此让通信兵带信回去,内容为(编号2,进攻时间2);
c) 负责通知将军3的通信兵被抓,因此将军3没收到参谋1的提议;
12) 参谋1收到了至少2个将军的回复,比较两个回复的编号大小,选择大编号对应的进攻时间作为最新的提议; 参谋1再次派通信兵带信给有答复的2个将军,内容为(编号3,进攻时间2);
13) 将军1和将军2收到了(编号3,进攻时间2),和自己保存的编号相同,因此保存(编号3,进攻时间2),同 时让通信兵带信回去,内容为(Accepted);
14) 参谋1收到了至少2个将军的(accepted)内容,确认进攻时间已经被多数派接受;
活锁
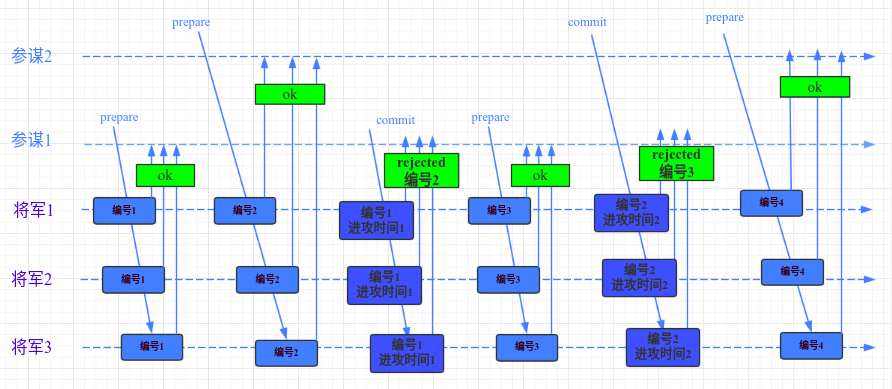
这里举一个极端的例子,
1)参谋1发送编号为1的prepare请求,所有的将军都接受到(其实只需要过半就行了),这是第一个prepare
2)参谋2发送编号为2的prepare请求,所有将军接收,承诺不再接收编号小于2的请求
3)参谋1发送编号为1的commit请求,所有将军接收以后,拒绝该commit请求。因为在 2)中他们承诺不接受编 号小于2的请求
4)参谋1放弃之前提案,增加编号,重新发送编号为3的prepare请求
5) 所有将军接收编号为3的prepare请求,并承诺不再赞成编号小于3的请求通过
6)参谋2发送的编号为2的commit请求到达所有将军处,但是他们拒绝改commit请求,因为在5)中将军们已经
承诺不赞成编号小于3的请求
7)参谋2放弃该提案,增加编号,重新发送编号为4的prepare请求
如果以上 4)~ 7) 步骤一直重复,也就是说:一个proposer的prepare请求被接收且通过,但是在它发起commit请求的之前,已经有编号更高的proposer发送prepare。那么它的commit请求就不能通过。 如果这个时间点刚好卡住,这种现象一直持续下去,那么永远也没有提案被通过,而且集群也一直在工作,陷入活锁状态。
4 为什么将accepted中编号最大请求的value返回
为了最终确定一个唯一的值,引入了acceptor集群。用大白话说,就是proposer和acceptor都做出了妥协(也就是两者的约束)。
对于proposer,它可以做出提案,但是其内容并不一定是自己最初想要提的。可以理解为只有第一个提案者,才能提出自己的观点,否则就要遵循别人的意志。 在prepare阶段,只有当proposer是第一个提案者或者Proposer的编号足够大时,才能继续。在第commit阶段,如果没有之前proposer的提案被接受(也就是说它的第一个提出议案的proposer),才能提出自己原本的提案,否则就要遵循别人的意志(已经被接收的accept[n,v]中n最大时对应的v)。
对于acceptor,在prepare阶段。它会无条件接受第一个提案prepare(n),但是每接受一个提案后都会做出承诺(不再接受编号小于n的prepare请求),然后返回accept[m,v],其中m在所有接受的accept请求中编号最大。在commit阶段,只要不违背承诺(accept[m,v],这里的m必须不小于n),就接受。 也就是收acceptor做出的承诺对于两个阶段都是同样有作用的。
当一个proposer发送commit请求,但是得到accepter的回复没有超过一半的时候,该proposer就没有确定一个值。 但是这个时候会在acceptor处留下一些Accept(n,v);可以理解为虽然它们的提案没有通过但是它们的意志还是留下来了。就是上面两段加粗了字体处。
先看下面的例子
三个proposer,五个acceptor。 其中proposer1提出了X方案,proposer2提出Y方案,proposer3提出Z方案。

2) 是第一个提案,acceptor1~3全部通过该prepare。 因为它们都没有accept过任何值(没有前人的意志,该proposer可以提自己的观点)
3) proposer1可以提出自己的方案X,发送accept(1,X)给accpetor1~3。
4)proposer2发送prepare(2)给acceptor3~5。
5) acceptor3~5全部通过proposer2的prepare请求,且没有前人意志。
5)proposer1将accept(1,X)发送给accceptor1~3。
6) first: accepter1~2通过了proposer的accept(1,X)方案。
second: acceptor3因为向proposer2承诺不接受比2小的提案,所以accept(1,X)方案没有通过。
这个时候,proposer1提出的方案X失败了,但是在acceptor1~2处留下了自己的意志。
7)proposer2提出自己的提案,发送accept(2,Y)给acceptor3~5。
8) first: acceptor4~5收到accept(2,Y)
second: 发送给acceptor3的accept(2,Y)因为网络拥塞没有到达
其结果就是proposer2的提案没有通过,但是其意志留着acceptor4~5
9) proposer3发送prepare(3)给acceptor1,acceptor3,acceptor5
10) acceptor1,acceptor3,acceptor5通过该prepare请求,
同时proposer1返回了accept(1,X)。preposer5返回了accept(2,Y)。 也就是返回了两种不同的意志。
11) proposer3比较了两种意志,然后选择编号最大的accept(2,Y)。
这里如果是proposer,acceptor数量都很多,可能会有很多的“意志”被留下。这里每次都是选择编号最大的所对应的提案。也就是之前所说的妥协,该提案者提出的议案内容用的是前者的。用的是递增的归纳,如果选择小的,就不能满足文章中的P2约束。
如果要用大白话强行解释一波的话: 因为每次发动accept(n,v)的时候,都可能会有先前的意志,如果有accpet(m,value)被最终确定了,那么m一定是所有acceptor接受到的accept中编号最大的,这样后续其他proposer再次发动提案的时候,一定会遵循accept(m,value)的意志(因为它得到了大部分人的认可,一定会有一个acceptor将它的意志返回给后续提案的人)。所以m所对应的value就会传达到每一个存活的proposer(就是说proposer没有宕机)。
至于为什么prepare,commit阶段都选择大于先前承诺的n,而不是小于n。 这个可以说是这么规定的。如果一定要钻牛角尖的话。不妨这样解释:数学归纳法都是由前面往后面归纳的(也就是从小到大)。 当然,你从大到小也是可以的,不过在编程实现的时候,编号要用先去规定的数字不断往下取。从每个方面来说都不符合正常的逻辑思维。
发送accept(3,Y)给acceptor1,acceptor2,acceptor5
12) acceptor1,acceptor2,acceptor5 都通过了accept(3,Y)。
13) proposer3收到过半的响应,确定了唯一的提案Y。
此后,如果proposer1,proposer2再次去发起提案,最后得到的结果都是Y。
后面只要有提案被接收,它的值一定和之前被确定的值相同。
但是还有一个问题: 如果中途有proposer宕机,然后等它恢复的时候,这轮投票已经结束了(这是Multi-Paxos的经典问题)。这个时候learner角色的作用就出现了。
三 Learning a Chosen Value
To learn that a value has been chosen, a learner must find out that a pro-
posal has been accepted by a majority of acceptors. The obvious algorithm
is to have each acceptor, whenever it accepts a proposal, respond to all
learners, sending them the proposal. This allows learners to find out about
a chosen value as soon as possible, but it requires each acceptor to respond
to each learner—a number of responses equal to the product of the number
of acceptors and the number of learners.
The assumption of non-Byzantine failures makes it easy for one learner
to find out from another learner that a value has been accepted. We can
have the acceptors respond with their acceptances to a distinguished learner,
which in turn informs the other learners when a value has been chosen. This
approach requires an extra round for all the learners to discover the chosen
value. It is also less reliable, since the distinguished learner could fail. But
it requires a number of responses equal only to the sum of the number of
acceptors and the number of learners.
More generally, the acceptors could respond with their acceptances to some set of distinguished learners, each of which can then inform all the learners when a value has been chosen. Using a larger set of distinguished learners provides greater reliability at the cost of greater communication complexity.
Because of message loss, a value could be chosen with no learner ever finding out. The learner could ask the acceptors what proposals they have accepted, but failure of an acceptor could make it impossible to know whether or not a majority had accepted a particular proposal. In that case, learners will find out what value is chosen only when a new proposal is chosen. Ifa learner needs to know whether a value has been
chosen, it can have a proposer issue a proposal, using the algorithm described above.
要知道一个已经被选定的值,一个leaner必须知道proposal已经把过半的acceptor接受且通过。最明显的算法是让每个acceptor在接受提案时对所有学习者做出响应,然后将提案发送给他们。这使learner能够尽快发现所选的值,但它要求每个接受者对每个学习者做出响应,但是响应的数量=acceptor数量 * learner数量。
假设这是非拜占庭模式(简答的说就是消息不会被篡改,可以丢失)。一个learner很容易从另一个learner那里发现一个值已经被接受。 我们可以让acceptor去响应一个master learner,当选择了一个值时,master learner又会通知其他learner。这种方法需要所有learner进行额外的一轮交流才能发现所选择的值。 它也不太可靠,msater learner可能会失败。 但是,它需要的响应数量 = acceptor数量 + learner数量。
更普遍的是,acceptor确认提案后,将提案发送给一个master learner集合(也就是多master)。 当一个值被选定时,这些master可以将消息通知其他leaner。 采用master learner集合可以提高可靠性,但是也增加了通信的复杂性。
由于消息丢失,可能一个值已经被选定了,而learner却没有发现。 learner可以向acceptor询问他们接受了哪些提议,但是一个acceptor如果失败,可能让learner无法知道已经有过半的acceptor接受了特定提议(比如集群总数是2*n+1,一个提案只要得到n+1个acceptor通过就可以被确定下来。但是如果有一个acceptor宕机,那就只有n个通过,没有超过一半)。在这种情况下,只有当新提案重新被选定,learner才能发现之前选择了什么值(上面那个例子,比如有一个宕机了,但是还有n个acceptor已经通过了它的提案,再次发起提案的时候,因为会发送给过半的acceptor,之前的意志还会被继承。所确定的值一定和之前选定的值相同)。 如果learner需要知道一个值是否已经被选定,可以使用上述算法让proposer从新发布提议。
四 Progress
It’s easy to construct a scenario in which two proposers each keep issuing
a sequence of proposals with increasing numbers, none of which are ever
chosen. Proposer p completes phase 1 for a proposal number n 1 . Another
proposer q then completes phase 1 for a proposal number n 2 > n 1 . Proposer
p’s phase 2 accept requests for a proposal numbered n 1 are ignored because
the acceptors have all promised not to accept any new proposal numbered
less than n 2 . So, proposer p then begins and completes phase 1 for a new
proposal number n 3 > n 2 , causing the second phase 2 accept requests of
proposer q to be ignored. And so on.
To guarantee progress, a distinguished proposer must be selected as the
only one to try issuing proposals. If the distinguished proposer can com-
municate successfully with a majority of acceptors, and if it uses a proposal
with number greater than any already used, then it will succeed in issuing a
proposal that is accepted. By abandoning a proposal and trying again if it
learns about some request with a higher proposal number, the distinguished
proposer will eventually choose a high enough proposal number.
If enough of the system (proposer, acceptors, and communication net-
work) is working properly, liveness can therefore be achieved by electing a
single distinguished proposer. The famous result of Fischer, Lynch, and Pat-
terson [1] implies that a reliable algorithm for electing a proposer must use
either randomness or real time—for example, by using timeouts. However,
safety is ensured regardless of the success or failure of the election.
这段文字主要描述的是活锁,在上面例子中已经写到了。就是两个proposer不断的发起proposal,而且每个proposal都只通过了阶段一,然后在第二阶段的时候因为acceptor承诺了更大的prepare(n)而不再接受。解决的方式是通过设置一个超时时间戳,比如一个提案失败了,并不会立马增大编号再次发动proposal,而是在一个随机的时间戳以后增大编号发动。 比如在确定一系列值的时候,在一轮选举以后,会有一个proposer的提案最先被通过,然后使用它作为master proposer再连续发起几个proposal。 这样做的好处是提高了效率,不需要每个提案都经过一次选举(这里可以近似民主和专治,所以proposer一起选举,有利于民主,但是选出一个提案需要花费更多的时间。如果由其中某一个人提案决定,也就是专治,选举一个提案的效率更高。不过民主参与度就降低了)。
五 Implementing a State Machine
A simple way to implement a distributed system is as a collection of clients that issue commands to a central server. The server can be described as a deterministic state machine that performs client commands in some sequence. The state machine has a current state; it performs a step by taking as input a command and producing an output and a new state. For example, the clients of a distributed banking system might be tellers, and the state-machine state might consist of the account balances of all users.
A withdrawal would be performed by executing a state machine command that decreases an account’s balance if and only if the balance is greater than the amount withdrawn, producing as output the old and new balances. An implementation that uses a single central server fails if that serverfails. We therefore instead use a collection of servers, each one independently implementing the state machine. Because the state machine is deterministic,
all the servers will produce the same sequences of states and outputs if they all execute the same sequence of commands. A client issuing a command can then use the output generated for it by any server.
To guarantee that all servers execute the same sequence of state machine commands, we implement a sequence of separate instances of the Paxos consensus algorithm, the value chosen by the i th instance being the i th state machine command in the sequence. Each server plays all the roles (proposer, acceptor, and learner) in each instance of the algorithm. For now, I assume that the set of servers is fixed, so all instances of the consensus algorithm use the same sets of agents.
In normal operation, a single server is elected to be the leader, which acts as the distinguished proposer (the only one that tries to issue proposals) in all instances of the consensus algorithm. Clients send commands to the leader, who decides where in the sequence each command should appear. If the leader decides that a certain client command should be the 135 th command, it tries to have that command chosen as the value of the 135 th
instance of the consensus algorithm. It will usually succeed. It might fail because of failures, or because another server also believes itself to be the leader and has a different idea of what the 135 th command should be. But the consensus algorithm ensures that at most one command can be chosen as the 135 th one.
Key to the efficiency of this approach is that, in the Paxos consensus algorithm, the value to be proposed is not chosen until phase 2. Recall that, after completing phase 1 of the proposer’s algorithm, either the value to be proposed is determined or else the proposer is free to propose any value.
I will now describe how the Paxos state machine implementation works during normal operation. Later, I will discuss what can go wrong. I consider
what happens when the previous leader has just failed and a new leader has been selected. (System startup is a special case in which no commands have yet been proposed.)
以下用一个简单的方法去实现一个分布式系统: 一系列客户端向中央服务发送命令。服务器可以描述为以一定顺序执行客户端命令的确定性状态机。状态机具有当前状态。它通过将命令作为输入并产生输出和新状态来执行步骤。例如,分布式银行系统的客户是柜员,并且状态机状态由所有用户的帐户余额组成。
银行提现可以被视为一系列状态机命令,该命令当且仅当余额大于提款金额时才减少帐户的余额,并产生旧余额和新余额作为输出。如果使用一台中央服务器,则该服务器可能宕机失败。因此,我们改为使用服务器集群,每个服务器有独立状态机。 因为状态机是确定性的,所以如果它们都执行相同的命令序列,则所有服务器将产生相同的状态序列和输出。 然后,发出命令的客户端可以使用任何服务器为其生成的输出。
为了确保所有服务器执行相同的状态机命令序列,我们实现了Paxos共识算法的不同实例序列(其实就是用多次basic-paxos),第i个实例选择的值是序列中的第i个状态机命令。 每个服务器在算法的每个实例中扮演所有角色(提议者,接受者和学习者)。 现在,我假设服务器组是固定的,因此共识算法的所有实例都使用相同的代理组。
在正常操作中,将选择一台服务器作为领导者,并在共识算法的所有实例中充当leader proposer(尝试发布提议的唯一提议者)。客户将命令发送给leader proposer,leader proposer决定每个命令应在顺序中出现的位置。如果leader proposer确定某个客户端命令应为第135条命令,则它将尝试选择该命令作为第135条命令的值。共识算法通常会成功。它可能由于选举失败而失败,或者因为另一台服务器也认为自己是leader proposer并且对第135条命令的含义有不同的决定。但是共识算法确保最多可以选择一个命令作为第135个命令。 这种方法的效率的关键在于,在Paxos共识算法中,直到第2阶段才选择要提出的值。回想一下,在完成提议者算法的第1阶段之后,要么确定了要提出的值,要么提议者可以自由提出任何价值。
现在,我将描述Paxos状态机实现在正常操作期间如何工作。稍后,我将讨论可能出问题的地方。考虑一下 当先前的领导者刚刚失败,并选择了新的领导者时会发生什么。 (系统启动是一种特殊情况,其中尚未提出任何命令。)
The new leader, being a learner in all instances of the consensus algorithm, should know most of the commands that have already been chosen. Suppose it knows commands 1–134, 138, and 139—that is, the values chosen in instances 1–134, 138, and 139 of the consensus algorithm. (We will see later how such a gap in the command sequence could arise.) It then executes phase 1 of instances 135–137 and of all instances greater than 139.
(I describe below how this is done.) Suppose that the outcome of these executions determine the value to be proposed in instances 135 and 140, but leaves the proposed value unconstrained in all other instances. The leader then executes phase 2 for instances 135 and 140, thereby choosing commands 135 and 140.
The leader, as well as any other server that learns all the commands the leader knows, can now execute commands 1–135. However, it can’t execute commands 138–140, which it also knows, because commands 136 and 137 have yet to be chosen. The leader could take the next two commands requested by clients to be commands 136 and 137. Instead, we let it fill the
gap immediately by proposing, as commands 136 and 137, a special “noop” command that leaves the state unchanged. (It does this by executing phase 2 of instances 136 and 137 of the consensus algorithm.) Once these no-op commands have been chosen, commands 138–140 can be executed.
新领导者是共识算法所有实例中的学习者,应该知道大多数已选择的命令。假设它知道命令1–134、138和139,即共识算法实例1–134、138和139中选择的值。 (我们将在后面看到如何在命令序列中出现这样的间隙。)然后,它执行实例135-137和所有大于139的实例的阶段1。(我在下面描述如何做到这一点。)假设这些执行的结果确定了实例135和140中要提出的值,但在所有其他实例中都不受约束。领导者然后对实例135和140执行阶段2,从而选择命令135和140。
领导者以及学习领导者知道的所有命令的任何其他服务器现在可以执行命令1–135。但是,它无法执行它也知道的命令138-140,因为尚未选择命令136和137。领导者可以将客户要求的接下来的两个命令作为命令136和137。相反,我们让它填充,通过建议使用特殊的“空转”命令(保持状态不变)作为命令136和137,立即消除间隙。 (它通过执行共识算法实例136和137的阶段2来完成。)一旦选择了这些无操作命令,就可以执行命令138-140。
Commands 1–140 have now been chosen. The leader has also completed phase 1 for all instances greater than 140 of the consensus algorithm, and it is free to propose any value in phase 2 of those instances. It assigns command number 141 to the next command requested by a client, proposing it as the value in phase 2 of instance 141 of the consensus algorithm. It proposes the next client command it receives as command 142, and so on.
The leader can propose command 142 before it learns that its proposed command 141 has been chosen. It’s possible for all the messages it sent in proposing command 141 to be lost, and for command 142 to be chosen before any other server has learned what the leader proposed as command 141. When the leader fails to receive the expected response to its phase 2 messages in instance 141, it will retransmit those messages. If all goes well,
its proposed command will be chosen. However, it could fail first, leaving a gap in the sequence of chosen commands. In general, suppose a leader can get α commands ahead—that is, it can propose commands i + 1 through i +α after commands 1 through i are chosen. A gap of up to α−1 commands could then arise
现在已选择命令1–140。领导者还为大于共识算法140的所有实例完成了阶段1,并且可以在那些实例的阶段2中随意提出任何值。它将命令号141分配给客户端请求的下一个命令,并建议将其作为共识算法实例141的阶段2中的值。它提出了接收到的下一个客户端命令作为命令142,依此类推。 领导者可以在获悉已选择其提议的命令141之前提出命令142。它在提议命令141中发送的所有消息都可能丢失,并且有可能在任何其他服务器了解领导者作为命令141提出的建议之前选择命令142。当领导者未能收到对其阶段2的预期响应时在实例141中的消息,它将重传那些消息。如果一切顺利,将选择其建议的命令。但是,它可能首先失败,从而在选择的命令序列中留下空白。通常,假设领导者可以提前获得α命令-也就是说,在选择命令1至i之后,它可以提出命令i + 1至i +α。然后可能出现多达α-1个命令的间隙。
A newly chosen leader executes phase 1 for infinitely many instances of the consensus algorithm—in the scenario above, for instances 135–137 and all instances greater than 139. Using the same proposal number for all instances, it can do this by sending a single reasonably short message to the other servers. In phase 1, an acceptor responds with more than a simple OK only if it has already received a phase 2 message from some proposer. (In the scenario, this was the case only for instances 135 and 140.) Thus, a server (acting as acceptor) can respond for all instances with a single reasonably short message. Executing these infinitely many instances of phase 1 therefore poses no problem.
Since failure of the leader and election of a new one should be rare events, the effective cost of executing a state machine command—that is, of achieving consensus on the command/value—is the cost of executing only phase 2 of the consensus algorithm. It can be shown that phase 2 of the Paxos consensus algorithm has the minimum possible cost of any algorithm for reaching agreement in the presence of faults [2]. Hence, the Paxos algorithm is essentially optimal.
新选择的领导者对无限多个共识算法实例执行第1阶段-在上述情况下,对于实例135-137和大于139的所有实例。对所有实例使用相同的投标编号,它可以通过发送单个提案编号合理地向其他服务器发送短消息。在阶段1中,仅当接受者已经从某个提议者那里接收到阶段2消息时,它才会以简单的OK做出响应。 (在这种情况下,只有实例135和140才是这种情况。)因此,服务器(充当接受者)可以使用以下命令对所有实例进行响应 一条合理的短消息。因此,执行这些无限多个阶段1实例不会造成任何问题。
由于领导者的失败和新任总统的选举很少事件,执行状态机命令的有效成本(即,对命令/值达成共识)是仅执行共识算法第2阶段的成本。可以证明,Paxos共识算法的第2阶段在出现故障的情况下具有达成共识的任何算法的最小可能成本[2]。因此,Paxos算法本质上是最佳的。
This discussion of the normal operation of the system assumes that there is always a single leader, except for a brief period between the failure of the current leader and the election of a new one. In abnormal circumstances, the leader election might fail. If no server is acting as leader, then no new commands will be proposed. If multiple servers think they are leaders, then they can all propose values in the same instance of the consensus algorithm, which could prevent any value from being chosen. However, safety is preserved—two different servers will never disagree on the value chosen as the i th state machine command. Election of a single leader is needed only to ensure progress.
If the set of servers can change, then there must be some way of determining what servers implement what instances of the consensus algorithm. The easiest way to do this is through the state machine itself. The current set of servers can be made part of the state and can be changed with ordinary state-machine commands. We can allow a leader to get α commands
ahead by letting the set of servers that execute instance i + α of the consensus algorithm be specified by the state after execution of the i th state machine command. This permits a simple implementation of an arbitrarily sophisticated reconfiguration algorithm.
对系统正常运行的讨论假设只有一个领导者,除了在当前领导者失败和选举新领导者之间的短暂时间之外。在异常情况下,领导人选举可能会失败。如果没有服务器充当领导者,则不会提出新命令。如果多个服务器认为自己是领导者,那么它们都可以在共识算法的同一实例中提出值,这可能会阻止选择任何值。但是,安全性得以保留-两个不同的服务器将永远不会在选择作为第i个状态机命令的值时发生分歧。仅需选举一位领导才能确保取得进展。
如果服务器组可以更改,那么必须有某种方法来确定哪些服务器实现共识算法的哪些实例。最简单的方法是通过状态机本身。当前服务器集可以成为状态的一部分,并且可以使用普通的状态机命令进行更改。我们可以允许领导者获得α命令,通过让执行第i个状态机命令后的状态指定执行共识算法的实例i +α的服务器集来提前。这允许任意复杂的重新配置算法的简单实现。