二叉树前序中序后序遍历的迭代实现

前言

二叉树的前序、中序、后序遍历用递归实现较为简单。

在阅读他人代码时，发现有人用迭代方式实现，因此想扩展下自己。

二叉树有前序、中序、后序、层次遍历四种。

下面的结点按照访问的顺序标号，从左到右顺序依次是后序、前序、中序、层次遍历

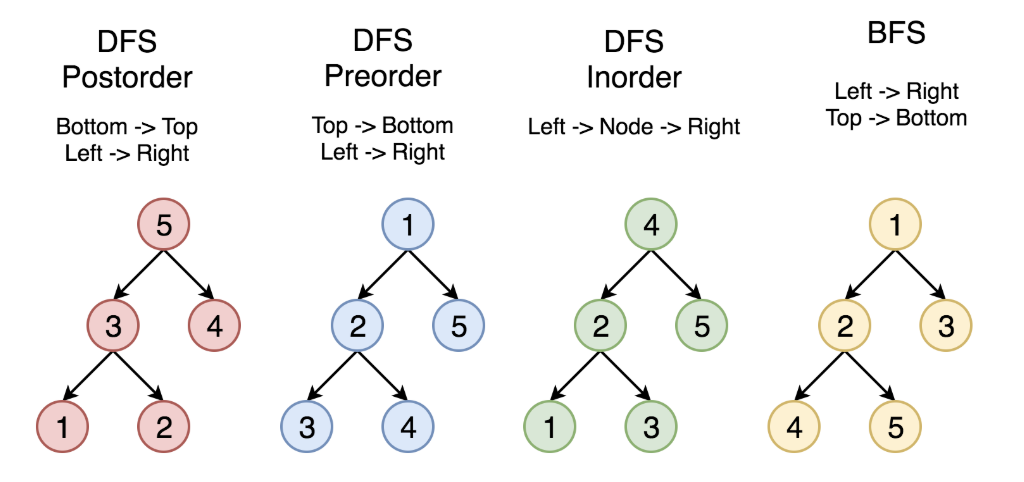
如标题所述，这里只讲前序、中序、后序迭代遍历

前序

借用栈的结构，先后将右子树和左子放入栈中，利用栈后入先出的原理遍历。

1. 借用栈的结构
2. 先push(root)
3.1 出栈 node = st.top(); st.pop()
3.2 记录当前值 res.push_back(p->val);
3.3 将右子树入栈 push(p->right)
3.4 将左子树入栈 push(p->left)
4. 循环步骤3直到栈空

vector<int> preorderTraversal(TreeNode *root) {
     vector<int> res;
     if(!root) return res;
     stack<TreeNode*> st;
     st.push(root);
     
     while(!st.empty()){
         TreeNode* p = st.top();
         res.push_back(p->val);
         st.pop();
         if(p->right) st.push(p->right);
         if(p->left) st.push(p->left);
     }
     return res;
 }

中序

当前节点有左子节点时，将当前节点压栈，并将左子节点作为当前处理；当前节点无左子节点时，表示左子树都已遍历完成，此时访问当前节点，并将右子节点设为当前节点。

1. 借用栈的结构
2. 把root、以及root左孩子都压入栈中
3.1 出栈 root = st.top(); st.pop();
3.2 记录当前值 res.push_back(root->val);
3.3 将右子节点设为当前节点 root = root->right;
4. 循环步骤2直到栈为空且root为null

vector<int> inorderTraversal(TreeNode* root) {
    stack<TreeNode*> st;
    vector<int> res;
    while (!st.empty() || root != NULL) {
        while (root != NULL) {
            st.push(root);
            root = root->left;
        }
        root = st.top(); st.pop();
        res.push_back(root->val);
        root = root->right;
    }
    return res;
}

后序

当前节点被读取的条件为: 无左右孩子，或者上一次读取的为其左右孩子。否则按照先右后左的方式对子节点压栈。

vector<int> postorderTraversal(TreeNode *root){
    vector<int> res;
    if(!root) return res;
    stack<TreeNode *> st;
    TreeNode * pre = nullptr;
    st.push(root);
    while(!st.empty()){
        TreeNode * p = st.top();
        if((!p->left && !p->right) || 
            (pre && (pre == p->left || pre == p->right))) {
            res.push_back(p->val);
            st.pop();
            pre = p;
        }
        else{
            if(p->right) st.push(p->right);
            if(p->left) st.push(p->left);
        }
     }
     return res;        
 }

后序遍历有一种巧妙的方式：前序遍历根节点，先后将左右子节点压栈。这样的遍历顺序为: 中，右，左。最后reverse结果，则遍历结果变为: 左，右，中。

vector<int> postorderTraversal(TreeNode *root){
    vector<int> res;
    if(!root)  
        return res;
    stack<TreeNode *> st;
    st.push(root);
    while(!st.empty()){
        TreeNode * p = st.top();
        res.push_back(p->val);
        st.pop();
        if(p->left) st.push(p->left);
        if(p->right) st.push(p->right);
    }
    reverse(res.begin(), res.end());
    return res;        
}

参考链接

ubuntu咸鱼

二叉树前序中序后序遍历的迭代实现

前言

前序

中序

后序

Search

Table of Contents